Anomália detektálás saját megoldással #2

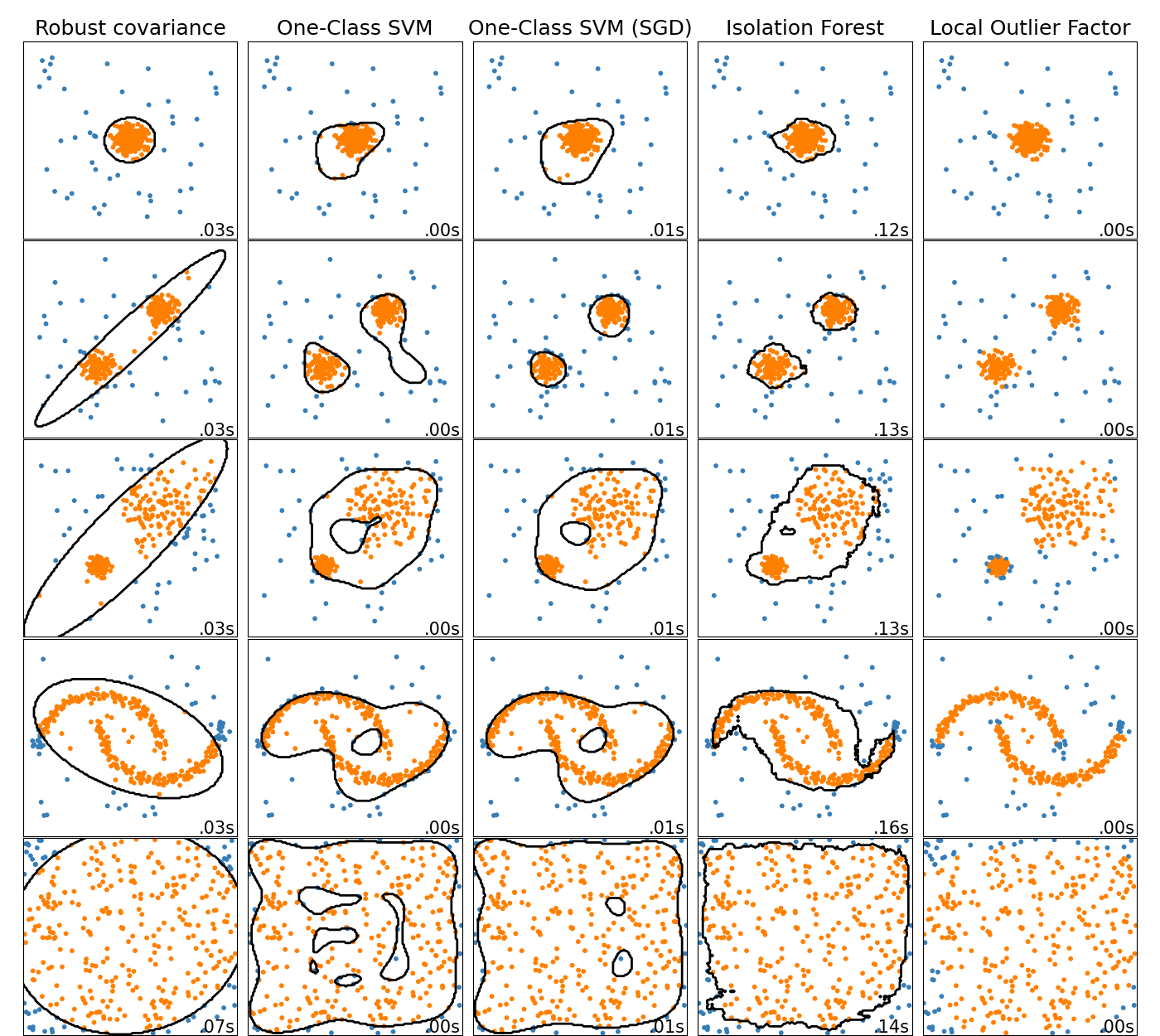
Forrás: https://scikit-learn.org/stable/auto_examples/miscellaneous/plot_anomaly_comparison.html

Előző blogomban leírtam a működését az új eljárásomnak. Be szeretném mutatni az előnyeit, és hogy miért probléma sokszor a sztochasztikus működés más megoldás esetén.

ISOLATION FOREST

Nézzünk pár bizonyítékot a sztochasztikus eljárás és az izolációs erdő eljárásának problémájára. Az alábbi eredmény az anomália indexét és "erősségét" mutatja, legfelül a legerősebbekkel.

1000 x 10-es mátrix 1/rand véletlen értékkel töltve, mely ezzel erős kiugrásokat tartalmaz. Ennél mindkét eljárás megtalálja a fő anomáliákat:

d = (1..1000).map{ (1..10).map{ 1/rand }};

anomaly d
=> [[840, 0.795451093344068],
[316, 0.7590785976282702],
[853, 0.7454339542758848],
[231, 0.7192541289754559],
[502, 0.7187162802019861],
[767, 0.6976003534785414],
[102, 0.6379026369941259],
[201, 0.6331330212736175],
[97, 0.6013006860292524],
[868, 0.6011251209945649]]

anomaly2 d
=> [[840, 8.11095548064013],
[201, 5.061092985687855],
[316, 4.372898022288503],
[853, 4.18506824782743],
[502, 3.3748958163853846],
[231, 3.3504088500722364],
[868, 3.2651277428023757],
[767, 3.14422193354402],
[770, 3.019286681059155],
[97, 3.0014224544240875]]

Az első az IF eredménye, ahol ő egy 0.6 feletti pontszámot mutat arra, hogy mennyire erős az anomália. Én pedig szigma értéket teszek mellé.

Nézzünk egy magasabb dimenziójú 1000 x 100-as mátrixot, ahol minden értéket rand-al töltök fel, ami egy 0..1 közötti érték, végig "kisimítva azt", kivéve az első sor első elemét, ahová 999 értéket teszek. Egyértelműen erős devianciát okozva:

d = (1..1000).map{ (1..100).map{ rand }}; d[0][0] = 999;

anomaly d
=> []

anomaly2 d
=> [[0, 27.79480077723804]]

Miért nem találja meg a 0-ás indexet az IF algo? (Többször futtatva sem teszi.) Látható ebből, hogy gond tud lenni, ha az eljárás szempontjából a bizonytalansági tényező az eredmény megtalálására nem közel nulla.

További probléma IF megoldással, hogy nem határozható meg egyértelműen, hogy a 0.6 feletti pontszámnál hol húzzuk meg a határt. Saját megoldásomnál ez egyértelműen definiálható statisztikailag a szigma értékkel, mely sokkal jobb referencia pont.

Másik hiba az IF eredményében:

LOCAL OUTLIER FACTOR

Itt szintén probléma a határérték egyértelműsíthetetlensége:

https://en.wikipedia.org/wiki/Local_outlier_factor

„The resulting values are quotient-values and hard to interpret. A value of 1 or even less indicates a clear inlier, but there is no clear rule for when a point is an outlier. In one data set, a value of 1.1 may already be an outlier, in another dataset and parameterization (with strong local fluctuations) a value of 2 could still be an inlier.”

Ezen kívül rengeteg hiperparaméter van, melyek megfelelő meghatározására nem ismert eljárás, főleg címkézett adat nélkül, ami alap igény AD megoldás esetén:

https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.LocalOutlierFactor.html

Kezdve az „n_neighbors” paraméterrel, ami az egyik legfontosabb. Ezek kívül a „leaf_size” is probléma.

ONE-CLASS SVM

SVM-nél szintén rémálom a hiperparaméter állítás. A „gamma” eleve probléma, mert erősen befolyásolja az eredményt. Az „auto” beállítás csak a változók számának reciproka, tehát nincs konkrét matematikai támogatás mögötte.

Bizonyos kernelek pedig még több ismeretlent behoznak, lásd:

https://scikit-learn.org/stable/modules/generated/sklearn.svm.OneClassSVM.html

ROBUST COVARIANCE

N dimenziós elliptikus illesztést csinál, ami eleve hibás sok alap problémánál. A valós gyakorlat nem írható le ilyen szépen szinte soha.

Megoldásom előnye az, hogy nem kell állítani paramétereket és mindig konzisztens eredményt ad, megtalálva minden devianciát. Matematikailag stabil az anomália határértékének maghatározása.