- carlcolt blogja
- A hozzászóláshoz be kell jelentkezni
- 322 megtekintés
Hozzászólások
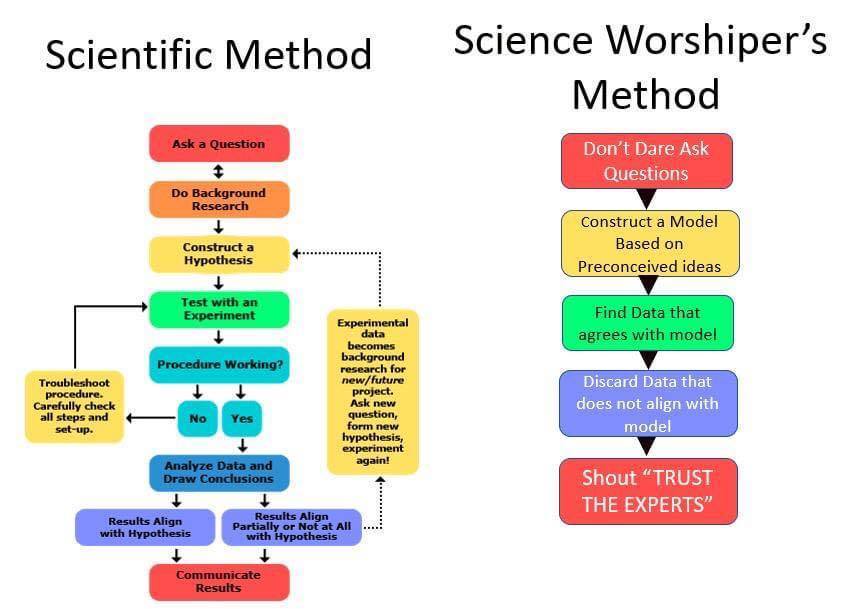
Nice. Kapásból három hiba is van rajta, A visszalinkelésnél nincs publikálás a hibás eredménynél, így mások a háttérkutatásban nem tudják felhasználni. A jó eredmény, nincs visszalinkelve a háttérkutatásba vagy a kérdésfeltevésbe. Az eredmény kommunikálása előtt nincs peer review, ezért a hibás, de jónak tűnő analízis eredménye is jóként lesz publikálva.
"Maradt még 2 kB-om. Teszek bele egy TCP-IP stacket és egy bootlogót. "
- A hozzászóláshoz be kell jelentkezni
No látod, mennyivel kevesebb a hibalehetőség a Scientific Worshipper's Method esetén.
"Normális ember már nem kommentel sehol." (c) Poli
- A hozzászóláshoz be kell jelentkezni
A másik topikba beírt linked alapján jutottam el e topikba.
Itt sincs semmi ellentmondás. Igaz mindkét ábra. A bal oldali vonatkozik a programozás hétköznapjaira, a „hasznossági” azaz utilitarista okokból (szempontok szerint) készített programokra, projectekre. (bár még azokra se mindig... erre jó példa amikor az M$ a csempés asztalt erőltette rá minden termékére egy teljesen agyament előzetes koncepcióból kiindulva).
A jobboldali ábra meg a programozás művészi oldalára vonatkozik. Beleértve ebbe természetesen a magam Peri nyelvét is, ezt sietve elismerem, azaz felesleges emiatt gúnyolódni bárkinek is! Így van, a Peri arra az oldalra illik!
Na most mindkét oldalnak megvan a maga HASZNA is. A jogosultsága. A bal oldali módszerrel nyilván előbb lehet hasznos(abb) programokat fejleszteni, többet és hatékonyabbat.
A jobb oldali módszer esetén az alkotások messze többsége haszontalan selejt lesz. Igenám, de mert ott szabadon szárnyalhat a képzelőerő, emiatt épp AZ az oldal az, ahol a váratlan, nagy felfedezések születhetnek, a szemkápráztató újítások, amiket aztán felkarolhat a „bal” oldal is, továbbfejlesztve, kijavítva a kezdeti tökéletlenségeket...
- A hozzászóláshoz be kell jelentkezni
Jo felvetes, kapasbol 3 ponton hibas.
Kommunikalasrol van szo, nem publikalasrol.
A peer review a kommunikalas utan tortenik.
Sehol nem irta, hogy "jokent" lesz kommunikalva.
Lambda calculus puts the fun into functional programming
- A hozzászóláshoz be kell jelentkezni
Kommunikálás/publikálás előtt érdemes zárt vagy előzetes peer reviewnak alávetni, így nem maradnak olyan hibák benne, mint az én postomban. ;)
"Maradt még 2 kB-om. Teszek bele egy TCP-IP stacket és egy bootlogót. "
- A hozzászóláshoz be kell jelentkezni
Egyetertek. Az en meglatasom, hogy OP a kommunikalas alatt a tarsszerzoivel valo beszelgetest is erthette. :)
Lambda calculus puts the fun into functional programming
- A hozzászóláshoz be kell jelentkezni
Science worshipper's method: mintha csak a finnugoristákat látnám...
- A hozzászóláshoz be kell jelentkezni
Az a baj, hogy az abra jobb oldalan hibas az elnevezes. Ha tenyleg tisztelnek/imadnak a tudomanyt, akkor nem igy mukodnenek, es nem teljesen nyilvanvaloan hulyesegeket probalnanak bizonygatni.
TFM-nek volt egy vicces videoja (par eve, ez az ujra feltoltott valtozata), amiben ezt figurazta ki. De az is jo volt, amikor par eve kamu tanulmanyokat kuldtek el publikalasra kutatok, es volt, ami meg is jelent, mert illeszkedett a folyoiratok SJW temajaba.
A strange game. The only winning move is not to play. How about a nice game of chess?
- A hozzászóláshoz be kell jelentkezni
Az a baj, hogy egyetlen ember sem létezik a földön, aki bármilyen témában képes lenne a bal oldali flowt végigvinni. Olyan sok van, aki egy adott, meglehetősen szűk területen képes erre, de ha reálisan nézed, az ember ideje véges. Ha mondjuk te világelső vagy elméleti fizikában, attól még korántsem biztos, hogy megalapozottan tudnál állást foglalni abban, hogy az orosz vagy a kínai vakcina biztonságosabb-e.
És akkor az átlag userről nem beszéltünk.
- A hozzászóláshoz be kell jelentkezni
Valamit jól kifiguráz a "science worshipper method", de valószínűleg a "trust the experts" ellen akart állást foglalni az elkövető, pedig az nem is olyan rossz stratégia. Ha egy témában tényleg jó vagy, akkor tudod, hogy mennyi munka odáig eljutni, vagy akár jónak maradni (nem felejteni, követni a téma fejlődését, sőt, előre vinni azt), és ez ahhoz ugyan nem fog vezetni, hogy feltétlen bízzál a szakértőkben, de ahhoz igen, hogy ne bízzál a nem-szakértőkben, és hogy amikor nem bízol a szakértőkben, akkor nem nagyon van más választásod, mint saját magadnak szakértővé válni (beletanulni).
A The Cosmic Revolutionary's Handbook nagyon jól kifejt egy csomó mindent a tudományos módszerrel és a szakértőkkel kapcsolatban, és idézi a legtömörebb megfogalmazását annak, hogy miért ne bízz a nem-szakértőkben,
It is necessary to get behind someone, before you can stab them in the back.
(Sir Humphrey Appleby a Yes, Prime Minister c. BBC sorozatban)
- A hozzászóláshoz be kell jelentkezni
Nem vagyok tudományművelő, csak kedvelő/imádó, de: nekem hiányzik az antitézis a baloldalról.
- A hozzászóláshoz be kell jelentkezni
Antitézis alatt valami olyasmit értesz, hogy egy kísérlet választ két lehetőség közül, hogy melyik igaz?
A legtöbb statisztikai próba pl. nem tud ilyet, van egy nullhipotézis (pl. a mért adatsor x0 várható értékű σ szórású normális eloszlásból származik), és a próba csak arra képes, hogy ezt elvesse (azaz, ha a nullhipotézis igaz lenne, akkor nagyon valószínűtlen lenne az adott, mért adatsor). De ha ez bekövetkezik, akkor csak annyit fogsz tudni, hogy a minta nem x0 várható értékű σ szórású normális eloszlásból származik, azt nem, hogy az átlag más, a szórás más, vagy az eloszlás nem normális.
- A hozzászóláshoz be kell jelentkezni
Ez nem mindenhol igaz, nem mindenhol működik. Van egy elképzelés és megnézi az ellenkezőjét, mert ha azt röviden ki tudja zárni, akkor van értelme elindulni.
- A hozzászóláshoz be kell jelentkezni
De ez csak akkor működik, ha az ellenkezője valami egyszerű, nem? A fenti példában a hipotézis ellenkezőjét szinte lehetetlen lenne megnézni (akkora minta kellene, amiből már az egész eloszlás becsülhető).
- A hozzászóláshoz be kell jelentkezni